(本小题满分12分) 是首项
是首项 的等比数列,其前
的等比数列,其前 项和为Sn,且
项和为Sn,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,设
,设 为数列
为数列 的前
的前 项和,
项和,
求证:
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, .
.
(Ⅰ)求证:
 ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
(本小题满分15分)
已知函数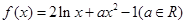
(Ⅰ)求函数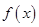 的单调区间;
的单调区间;
(Ⅱ)若 ,试分别解答以下两小题.
,试分别解答以下两小题.
(ⅰ)若不等式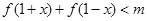 对任意的
对任意的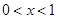 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(ⅱ)若 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
.
(本小题满分13分)
已知函数 ,其中
,其中 请分别解答以下两小题.
请分别解答以下两小题.
(Ⅰ)若函数过点 ,求函数
,求函数 的解析式.
的解析式.
(Ⅱ)如图,点 分别是函数
分别是函数 的图像在
的图像在 轴两侧与
轴两侧与 轴的两个相邻交点, 函数图像上的一点
轴的两个相邻交点, 函数图像上的一点 ,若满足
,若满足 ,求函数
,求函数 的最大值.
的最大值.
(本小题满分13分)如图,9个正数排列成3行3列,其中每一行的数成等差数列,每一列的数成等比数列,且所有的公比都是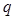 ,已知
,已知 ,
, 又设第一行数列的公差为
又设第一行数列的公差为 .
.
(Ⅰ)求出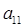 ,
, 及
及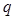 ;
;
(Ⅱ)若保持这9个数的位置不动,按照上述规律,补成一个n行n列的数表如下,试写出数表第n行第n列 的表达式,并求
的表达式,并求 的值.
的值.