已知 的图像与
的图像与 轴的交点为
轴的交点为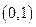 ,它在
,它在 轴右侧的第一个最大值和最小值点分别为
轴右侧的第一个最大值和最小值点分别为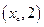 和
和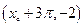
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(3)将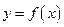 的图像上所有点的横坐标变为原来的
的图像上所有点的横坐标变为原来的 ,再将所得图像向右平移
,再将所得图像向右平移 个单位得函数
个单位得函数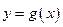 的图像,求
的图像,求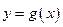 的解析式。
的解析式。
已知函数f(x)对于任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=- .
.
(1)求证:f(x)在R上是减函数.
(2)求f(x)在[-3,3]上的最大值和最小值.
已知f(x)= (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
已知a,b为常数,若f(x)=x2+4x+3,f(ax+b)=x2+10x+24,求5a-b的值.
如果对任意实数x,y,都有f(x+y)=f(x)·f(y),且f(1)=2,
(1)求f(2),f(3),f(4)的值.
(2)求 +
+ +
+ +…+
+…+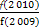 +
+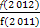 +
+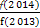 的值.
的值.
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p∨q”是假命题,求a的取值范围.