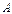
(本小题满分13分)已知函数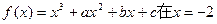 处取得极值,并且它的图象
处取得极值,并且它的图象
与直线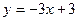 在点(1,0)处相切。
在点(1,0)处相切。
(Ⅰ)求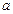 、
、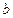 、
、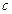 的值;
的值;
(Ⅱ)求函数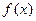 的单调区间。
的单调区间。
已知中心在原点,焦点在x轴上的椭圆C的离心率为 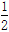 ,且经过点M
,且经过点M .
.
(1)求椭圆C的方程;
(2)是否存在过点P(2,1)的直线l1与椭圆C相交于不同的两点A,B,满足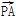 ·
· =
=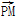 2?若存在,求出直线l1的方程;若不存在,请说明理由.
2?若存在,求出直线l1的方程;若不存在,请说明理由.
从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,
每次取出后不放回,连续取两次.
(1)求取出的两件产品中恰有一件次品的概率;
(2)如果将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的两件产品中恰有一件次品的概率是多少?
设命题p:实数x满足x2-4ax+3a2<0,其中a>0,命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
一个袋中有红、白两种球各若干个,现从中一次性摸出两个球,假设摸出的两个球至少有一个红球的概率为 ,至少一个白球的概率为
,至少一个白球的概率为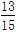 ,求摸出的两个球恰好红球白球各一个的概率.
,求摸出的两个球恰好红球白球各一个的概率.
已知抛物线
 上点
上点 到焦点
到焦点 的距离为4.
的距离为4.
(1)求 ,
, 值;
值;
(2)设 ,
, 是抛物线上分别位于
是抛物线上分别位于 轴两侧的两个动点,且
轴两侧的两个动点,且 (其中
(其中 为坐标原点).求证:直线
为坐标原点).求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.