(本小题满分14分)已知函数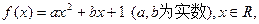

(1)若不等式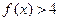 的解集为
的解集为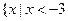 或
或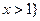 ,求
,求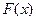 的表达式;
的表达式;
(2)在(1)的条件下, 当 时,
时,  是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设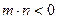 ,
, 
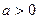 且
且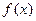 为偶函数, 判断
为偶函数, 判断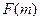 +
+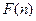 能否大于零?
能否大于零?
为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租。该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
已知
 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.
(I) 求 的函数表达式;
的函数表达式;
(II) 判断 的单调性, 并求出
的单调性, 并求出 的最小值.
的最小值.
已知函数
(1)求函数 的值域;
的值域;
(2)若 时,函数
时,函数 的最小值为
的最小值为 ,求
,求 的值和函数
的值和函数 的最大值。
的最大值。
已知函数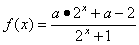 ,若函数
,若函数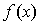 满足
满足 =-
=-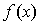
(1)求实数a的值。(2)判断函数的单调性
已知全集 ,
, .
.
(1)若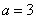 ,求
,求
(2)若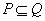 ,求实数
,求实数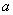 的取值范围
的取值范围