设函数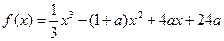 ,其中常数
,其中常数 >1。
>1。
(1)讨论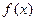 的单调性
的单调性
(2)若当 时,
时,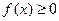 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(本小题满分12分)
如图,P—ABCD是正四棱锥,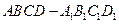 是正方体,其中
是正方体,其中

(1)求证: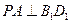 ;
;
(2)求PA与平面 所成角
所成角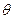 的余弦值;
的余弦值;
(本小题满分12分)
将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两枚骰子点数之和是3的倍数的结果有多少种?
(3)两枚骰子点数之和是3的倍数的概率为多少?
已知二次函数 同时满足:①不等式
同时满足:①不等式 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式 成立,设数列{
成立,设数列{ }的前
}的前 项和
项和 .
.
(1)求函数 的表达式;
的表达式;
(2) 设各项均不为0的数列{ }中,所有满足
}中,所有满足 的整数
的整数 的个数称为这个数列{
的个数称为这个数列{ }的变号数,令
}的变号数,令 (
(
 ),求数列{
),求数列{ }的变号数;
}的变号数;
(3)设数列{ }满足:
}满足: ,试探究数列{
,试探究数列{ }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.
已知 ,点
,点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;(Ⅱ)若直线
的方程;(Ⅱ)若直线 过点
过点 且与轨迹
且与轨迹 交于
交于 、
、 两点. (i)设点
两点. (i)设点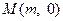 ,问:是否存在实数
,问:是否存在实数 ,使得直线
,使得直线 绕点
绕点 无论怎样转动,都有
无论怎样转动,都有 成立?若存在,求出实数
成立?若存在,求出实数 的值;若不存在,请说明理由.(ii)过
的值;若不存在,请说明理由.(ii)过 、
、 作直线
作直线 的垂线
的垂线 、
、 ,垂足分别为
,垂足分别为 、
、 ,记
,记 ,求
,求 的取值范围.
的取值范围.
)袋中装着标有数字1,2,3的小球各2个,从袋中任取2个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的2个小球上的数字互不相同的概率;
(Ⅱ)用 表示取出的2个小球上的数字之和,求随机变量
表示取出的2个小球上的数字之和,求随机变量 的概率分布与数学期望.
的概率分布与数学期望.