(理)已知函数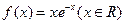
(1)求函数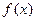 的单调区间和极值。
的单调区间和极值。
(2)已知函数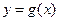 的图象与函数
的图象与函数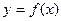 的图象关于直线
的图象关于直线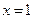 对称
对称
证明:当x>1时,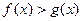 。
。
(3)如果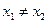 ,且
,且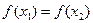 ,证明:
,证明: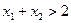
已知数列 是递增数列,且满足
是递增数列,且满足
(Ⅰ)若 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对于(Ⅰ)中 ,令
,令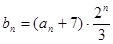 ,求数列
,求数列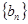 的前
的前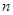 项和
项和 .
.
某商场准备在伦敦奥运会期间举行促销活动.根据市场行情,该商场决定从3种品牌的服装类商品、2种品牌的家电类商品、4种品牌的日用类商品中,任选出3种商品进行促销活动.
(Ⅰ)求选出的3种商品中至少有一种是日用类商品的概率;
(Ⅱ)商场对选出的家电类商品采用的促销方案是有奖销售,即在该类商品成本价的基础上每件提高180元作为售价销售给顾客,同时给该顾客3次抽奖的机会,若中奖一次,就可以获得一次奖金.假设该顾客每次抽奖时获奖的概率都是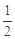 ,每次中奖与否互不影响,且每次获奖时的奖金数额都为
,每次中奖与否互不影响,且每次获奖时的奖金数额都为 元,求顾客购买一件此类商品时中奖奖金总额
元,求顾客购买一件此类商品时中奖奖金总额 的分布列和数学期望
的分布列和数学期望 ,并以此测算
,并以此测算 至多为多少时,此促销方案使商场不会亏本?
至多为多少时,此促销方案使商场不会亏本?
设函数 ·
· ,其中向量
,其中向量 ,
, ,
,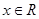 。
。
(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。
已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中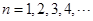
(1)证明:数列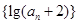 是等比数列;
是等比数列;
(2)设数列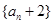 的前
的前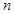 项积为
项积为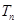 ,求
,求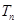 及数列
及数列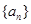 的通项公式;
的通项公式;
(3)已知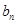 是
是 与
与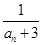 的等差中项,数列
的等差中项,数列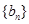 的前
的前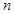 项和为
项和为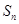 ,求证:
,求证: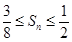 .
.
对于函数
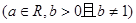
(1)判断函数的单调性并证明; (2)是否存在实数a使函数f (x)为奇函数?并说明理由.