(本小题满分12分)
已知四棱锥P—ABCD中,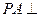 平面ABCD,底面ABCD为菱形,
平面ABCD,底面ABCD为菱形,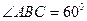 ,AB=PA=2,E、F分别为BC、PD的中点。
,AB=PA=2,E、F分别为BC、PD的中点。
(1)求证:PB//平面AFC;
(2)求平面PAE与平面PCD所成锐二面角的余弦值。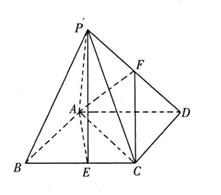
在△ 中,角
中,角 所对的边分别为
所对的边分别为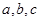 ,已知
,已知 ,
,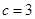 ,
, .(1)求
.(1)求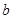 的值;(2)求
的值;(2)求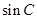 的值.
的值.
在甲、乙两个盒子中分别装有号为1、2、3、4的四个小球,现在从甲、乙两个盒子中各取出1个小球,每个小球被抽到的可能性相等。
(Ⅰ)求取出两个小球标号恰好相等的概率;
(Ⅱ)求取出的两个小球的标号至少有一个大于2的概率。
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下表格所示统计数据,由资料显示y对x呈线性相关关系。
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)请根据上表的数据画出散点图并用最小二乘法求出y关于x的线性回归方程?
(Ⅱ)试根据(1)求出的线性回归方程,预测使用年限为10年时,维修费用是多少?
以下茎叶图记录了甲,乙两个组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树为19的概率。
甲组 乙组
9 9 0 X 8 9
1 1 1 0
根据下面的要求,求 值。
值。
(Ⅰ)请完成执行该问题的程序框图;
(Ⅱ)用Do Loop循环语句描述这一算法