设命题 :“方程
:“方程 有两个实数根”;命题
有两个实数根”;命题 :“方程
:“方程 无实根”,若
无实根”,若 为假,
为假, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)求 ;
;
(Ⅱ)求函数 图象上的点
图象上的点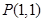 处的切线方程.
处的切线方程.
已知函数 ,
, ,
, ,其中
,其中 且
且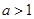 .
.
(I)求函数 的导函数
的导函数 的最小值;
的最小值;
(II)当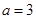 时,求函数
时,求函数 的单调区间及极值;
的单调区间及极值;
(III)若对任意的 ,函数
,函数 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
当 时,
时, ,
,
(I)求 ;
;
(II)猜想 与
与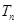 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: (
(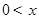 ≤120).已知甲、乙两地相距100千米。
≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?