(本小题满分10分)
已知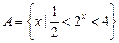 ,
, .
.
(1)求 和
和 ;
;
(2)定义运算 ,请在图中把表示“集合
,请在图中把表示“集合 ”的部分用阴影涂黑;并求
”的部分用阴影涂黑;并求 .
.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布 现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],...第6组[182.5,187.5],下图是按上述分组方法得到的频率分布直方图.
现从该省某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5]第二组[162.5,167.5],...第6组[182.5,187.5],下图是按上述分组方法得到的频率分布直方图.
(1)求该学校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上含(177.5cm)的人中任意抽取2人,该2人中身高排名(从高
到低)在全省前130名的人数记为 ,求
,求 的数学期望.
的数学期望.
参考数据:若 ~
~ .则
.则 ,
, ,
, .
.
已知数列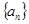 的前
的前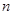 项和
项和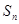 与通项
与通项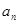 满足
满足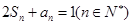 .
.
(1)求数列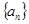 的通项公式;
的通项公式;
(2)数列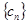 满足
满足 ,求证:
,求证: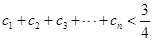 .
.
设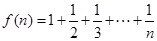 ,是否存在关于自然数n的函数
,是否存在关于自然数n的函数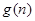 ,使等式
,使等式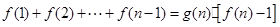 对于
对于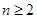 的一切自然数都成立?并证明你的结论.
的一切自然数都成立?并证明你的结论.
数列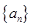 满足
满足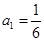 ,前n项和
,前n项和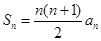 .
.
(1)写出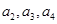 ;
;
(2)猜出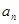 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
设 为一个三角形的三边,
为一个三角形的三边, ,且
,且 ,试证:
,试证: .
.