(本小题满分15分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市 的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B
的中点时,对城A和城B 的总影响度为0.065.
的总影响度为0.065.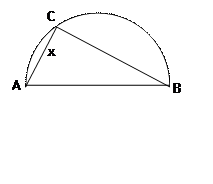
(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(本题10分)已知命题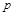 :
: <
< ,和命题
,和命题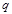 :
: ,
,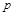

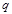 为真,
为真,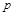
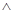
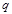 为假,求实数c的取值范围.
为假,求实数c的取值范围.
(本小题满分12分)已知二次函数 满足
满足 ,且
,且 .
.
(1)求 的解析式;
的解析式;
(2)若函数 的最小值为
的最小值为 ,求实数
,求实数 的值;
的值;
(3)若对任意互不相同的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数 .
.
(1)判断 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断 在
在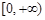 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(3)求满足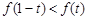 的
的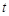 的取值范围.
的取值范围.
(本小题满分12分)某滨海高档住宅小区给每一户业主均提供两套供水方案.方案一是供应市政自来水,每吨自来水的水费是2元;方案二是限量供应10吨海底岩层中的温泉水,若温泉水用水量不超过5吨,则按基本价每吨8元收取,超过5吨不超过8吨的部分按基本价的1.5倍收取,超过8吨不超过10吨的部分按基本价的2倍收取.
(1)试写出温泉水用水费 (元)与其用水量
(元)与其用水量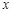 (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)若业主小王缴纳10月份的物业费时发现一共用水16吨,被收取的费用为72元,那么他当月的自来水与温泉水用水量各为多少吨?
(本小题满分12分)已知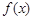 是定义在
是定义在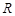 上的偶函数,且当
上的偶函数,且当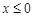 时,
时,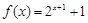 .
.
(1)求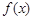 的解析式;
的解析式;
(2)在所给的坐标系内画出函数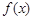 的草图,并求方程
的草图,并求方程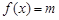 恰有两个不同实根时的实数
恰有两个不同实根时的实数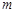 的取值范围.
的取值范围.