(文科)已知抛物线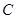 的顶点为原点,其焦点
的顶点为原点,其焦点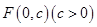 到直线
到直线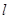 :
: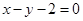 的距离为
的距离为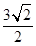 .设
.设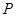 为直线
为直线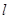 上的点,过点
上的点,过点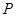 作抛物线
作抛物线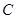 的两条切线
的两条切线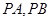 ,其中
,其中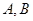 为切点.
为切点.
(Ⅰ)求抛物线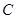 的方程;
的方程;
(Ⅱ)当点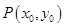 为直线
为直线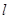 上的定点时,求直线
上的定点时,求直线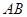 的方程;
的方程;
(Ⅲ)当点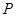 在直线
在直线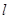 上移动时,求
上移动时,求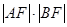 的最小值.
的最小值.
(理科)已知圆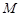 :
: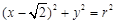 (
(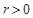 ).若椭圆
).若椭圆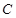 :
: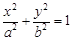 (
(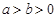 )的右顶点为圆
)的右顶点为圆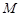 的圆心,离心率为
的圆心,离心率为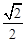 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆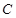 的方程;
的方程;
(Ⅱ)若存在直线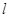 :
: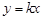 ,使得直线
,使得直线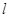 与椭圆
与椭圆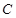 分别交于
分别交于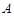 ,
,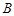 两点,与圆
两点,与圆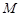 分别交于
分别交于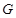 ,
,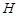 两点,点
两点,点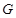 在线段
在线段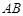 上,且
上,且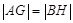 ,求圆
,求圆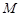 半径
半径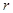 的取值范围.
的取值范围.
(文科)设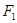 、
、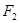 分别是椭圆
分别是椭圆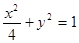 的左、右焦点.
的左、右焦点.
(Ⅰ)若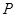 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求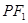 ·
·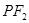 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点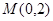 的直线
的直线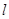 与椭圆交于不同的两点
与椭圆交于不同的两点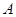 、
、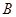 ,且∠
,且∠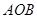 为锐角(其中
为锐角(其中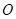 为坐标原点),求直线
为坐标原点),求直线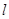 的斜率
的斜率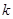 的取值范围.
的取值范围.
(文科)过点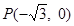 作直线
作直线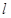 与椭圆
与椭圆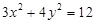 相交于
相交于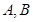 两点,
两点,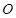 为坐标原点,求
为坐标原点,求 面积的最大值及此时直线倾斜角的正切值。
面积的最大值及此时直线倾斜角的正切值。
(理科)已知菱形 的顶点
的顶点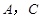 在椭圆
在椭圆 上,对角线
上,对角线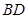 所在直线的斜率为1.
所在直线的斜率为1.
(Ⅰ)当直线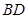 过点
过点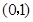 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)当 时,求菱形
时,求菱形 面积的最大值.
面积的最大值.