△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADB=30o,求AB,AC的长及△ABC的面积。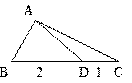
(本小题满分15分)
已知以点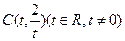 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
(Ⅰ)求证:△AOB的面积为定值;
(Ⅱ)设直线2x+y-4=0与圆C交于点M、N,若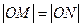 ,求圆C的方程;
,求圆C的方程;
(Ⅲ)在(Ⅱ)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求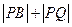 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。
(本小题满分15分)
设函数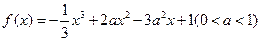 ,
,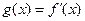 (其中
(其中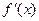 是函数
是函数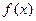 的导函数)
的导函数)
(Ⅰ)求函数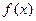 的极大值;
的极大值;
(II)若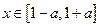 时,恒有
时,恒有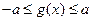 成立,试确定实数a的取值范围。
成立,试确定实数a的取值范围。
(本小题满分 分)
分)
(Ⅰ)若 是公差不为零的等差数列
是公差不为零的等差数列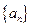 前n项的和,且
前n项的和,且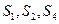 成等比数列,求数列
成等比数列,求数列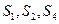 的公比;
的公比;
(II)设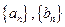 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,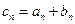 ,证明数列
,证明数列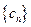 不是等比数列。
不是等比数列。
(本小题满分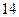 分)
分)
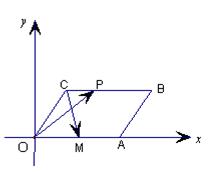
在平面直角坐标系xoy中,已知四边形OABC是平行四边形, ,点M是OA的中点,点P在线段BC上运动(包括端点),如图
,点M是OA的中点,点P在线段BC上运动(包括端点),如图
(Ⅰ)求∠ABC的大小;
(II)是否存在实数λ,使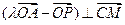 ?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。
?若存在,求出满足条件的实数λ的取值范围;若不存在,请说明理由。