一个袋中装有大小相同的黑球、白球和红球. 已知袋中共有10个球,从中任意摸出1个球,得到黑球的概率是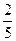 ,从中任意摸出2个球,至少得到1 个白球的概率是
,从中任意摸出2个球,至少得到1 个白球的概率是 . 求:
. 求:
(1)从中任意摸出2个球,得到的都是黑球的概率;
(2)袋中白球的个数
(本小题满分14分)
椭圆C: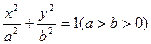 的两个焦点为
的两个焦点为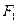 、
、 ,点
,点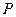 在椭圆C上,且
在椭圆C上,且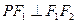 ,
,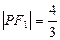 ,
,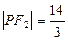 .
.
(1) 求椭圆C的方程;
(2) 若直线 过圆
过圆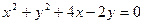 的圆心
的圆心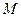 ,交椭圆C于
,交椭圆C于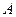 、
、 两点,且
两点,且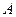 、
、 关于点
关于点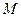 对称,求直线
对称,求直线 的方程.
的方程.
(本小题满分12分)
已知函数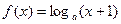 ,
,
(1)求函数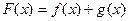 的定义域;
的定义域;
(2)判断函数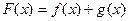 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(本小题满分14分)
在长方体 中,
中, 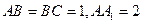 ,
,
(1) 求证: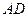 ∥面
∥面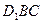 ;
;
(2) 证明: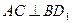 ;
;
(3) 一只蜜蜂在长方体 中飞行,求它飞入三棱锥
中飞行,求它飞入三棱锥 内的概率.
内的概率.
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
15 |
① |
| 第2组 |
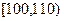 |
② |
0.35 |
| 第3组 |
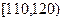 |
20 |
0.20 |
| 第4组 |
 |
20 |
0.20 |
| 第5组 |
 |
10 |
0.10 |
| 合计 |
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
已知 ,
,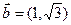
(1)若 ,求tan x;
,求tan x;
(2)若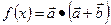 ,求
,求 的最大值.
的最大值.