已知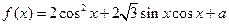 ,
,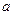 为实常数。
为实常数。
(I)求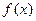 的最小正周期;
的最小正周期;
(II)若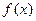 在
在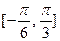 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求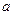 的值。
的值。
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
已知在递增等差数列{an}中,a1=2,a1,a3,a7成等比数列,{bn}的前n项和为Sn,且Sn=2n+1-2.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=abn,求数列{cn}的前n项和Tn.
已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列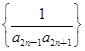 的前n项和.
的前n项和.
已知函数f(x)=sin2 +
+ sin
sin
 -
- .
.
(1)在△ABC中,若sin C=2sin A,B为锐角且有f(B)= ,求角A,B,C;
,求角A,B,C;
(2)若f(x)(x>0)的图象与直线y= 交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.
交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.
已知函数f(x)=2sin2 -
- cos 2x-1(x∈R).
cos 2x-1(x∈R).
(1)若函数h(x)=f(x+t)的图象关于点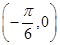 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;
(2)设p:x∈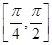 ,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.