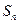 =1+
=1+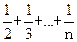 (n>1,n∈N),求证:
(n>1,n∈N),求证: (
(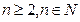 )
)
在数列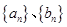 中,已知
中,已知 ,
, ,
,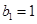 ,
,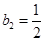 ,数列
,数列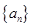 的前
的前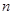 项和为
项和为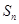 ,数列
,数列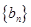 的前
的前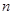 项和为
项和为 ,且满足
,且满足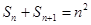 ,
, ,其中
,其中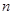 为正整数.
为正整数.
(1)求数列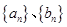 的通项公式;
的通项公式;
(2)问是否存在正整数 ,
,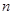 ,使
,使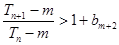 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对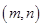 ,若不存在,请说明理由.
,若不存在,请说明理由.
已知椭圆 的上顶点为
的上顶点为 ,直线
,直线 交椭圆于
交椭圆于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 .
.
(1)若 时,求
时,求 的值;
的值;
(2)若 时,证明直线
时,证明直线 过定点.
过定点.
某公司生产的某批产品的销售量 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用 万元满足
万元满足 (其中
(其中 为正常数).已知生产该批产品还要投入成本
为正常数).已知生产该批产品还要投入成本 万元(不包含促销费用),产品的销售价格定为
万元(不包含促销费用),产品的销售价格定为 元/件.
元/件.
(1)将该产品的利润 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该公司的利润最大?
如图,过四棱柱 形木块上底面内的一点
形木块上底面内的一点 和下底面的对角线
和下底面的对角线 将木块锯开,得到截面
将木块锯开,得到截面 .
.
(1)请在木块的上表面作出过 的锯线
的锯线 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形时矩形 ,试证明:平面
,试证明:平面 平面
平面 .
.
已知向量 .
.
(1)当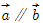 时,求
时,求 的值;
的值;
(2)设函数 ,当
,当 时,求
时,求 的值域.
的值域.