

11. (2009年高考辽宁卷)
如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰 角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01 km,
角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01 km,
≈1.414,≈2.449).
(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD= .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
[15,25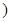 |
[25,35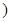 |
[35,45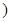 |
[45,55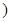 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 |
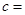 |
|
| 不赞成 |
 |
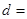 |
|
| 合计 |
(2)若对在[15,25) ,[25,35)的被调查中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为 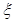 ,求随机变量
,求随机变量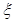 的分布列。
的分布列。
附:

(本小题共12分)
已知△ABC的角A,B,C的对边依次为a,b,c,若满足 ,
,
(1)求∠C大小;
(2)若c=2,且△ABC为锐角三角形,求a+b取值范围。
已知函数
(1)求函数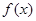 的单调区间和值域。
的单调区间和值域。
(2)设 ,求函数
,求函数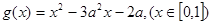 ,若对于任意
,若对于任意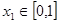 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数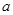 的取值范围。
的取值范围。
已知椭圆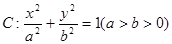 的右焦点为
的右焦点为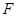 ,离心率
,离心率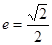 ,椭圆
,椭圆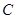 上的点到
上的点到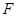 距离的最大值为
距离的最大值为 ,直线
,直线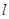 过点
过点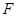 与椭圆
与椭圆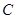 交于不同的两点
交于不同的两点 。
。
(1)求椭圆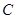 的方程。
的方程。
(2)若 ,求直线
,求直线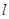 的方程。
的方程。