..(满分8分)已知数列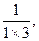
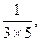

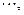
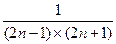 ,
,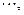
(1)计算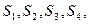
(2)根据(1)的计算结果,猜想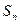 的表达式
的表达式 ,并用数学归纳法进行证明。
,并用数学归纳法进行证明。
(本小题满分10分)
在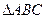 中,角
中,角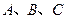 所对的边分别为
所对的边分别为 ,向量
,向量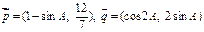 ,且
,且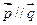 .
.
(Ⅰ)求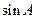 的值;
的值;
(Ⅱ)若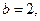
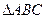 的面积为
的面积为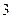 ,求
,求 .
.


.(本小题12分)
某车间为了规定工时定额,需要 确定加工零件所花费的时间,为此作了四次试验如下:
确定加工零件所花费的时间,为此作了四次试验如下:
零件的个数 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散 点图;
点图;
(2)求 关于
关于 的线性回归方程
的线性回归方程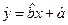 ;
;
(3)试预测加工10个零件需要多少时间?附: ,
,

本小题12分)
调查某地区老年人是否需要志愿者帮助,用简单随机抽样方法从该地调查500位老年人,结果如下:
| 性别 是否需要 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
① 估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
估计该地区老年人中,需要志愿者提供帮助的老年人的比例。
②能否有99%的把握认为该地区的老年人是否需要志愿者 提供帮助与性别有关?
提供帮助与性别有关?
附:
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |

(本题12分)
如图:△ABC的角平分线AD的延长线交它的外接圆于点E。
①证明:AB ·AC=AD·AE;
·AC=AD·AE;
②若△ABC的面积S=  AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。