(本小题满分12分)
如图,已知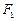 ,
, 分别是椭圆
分别是椭圆 :
: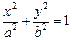 (
( )的左、右焦点,且椭圆
)的左、右焦点,且椭圆 的离心率
的离心率 ,
,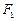 也是抛物线
也是抛物线 :
: 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 交椭圆
交椭圆 于
于 ,
, 两点,且
两点,且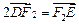 ,点
,点 关于
关于 轴的对称点为
轴的对称点为 ,求直线
,求直线 的方程.
的方程.
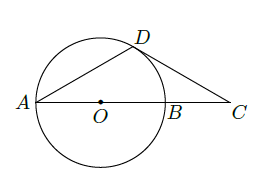
(1)几何证明选讲
是
的直径,
为
上一点,过点
作
的切线交
延长线于
,若
,求证
. 
(2)矩阵与变换
在平面直角坐标系
中,
,设
,
,点
在矩阵
对应的变换下得到点
的面积是
面积的2倍,求实数
的值
(3)参数方程与极坐标
在极坐标系中,圆
与直线
相切,求实数
的值.
(4)不等式证明选讲
已知实数
,求证:
.
设
使定义在区间
上的函数,其导函数为
.如果存在实数
和函数
,其中
对任意的
都有
,使得
,则称函数
具有性质
.
(1)设函数
,其中
为实数
①求证:函数
具有性质
;
②求函数
的单调区间
(2)已知函数
具有性质
,给定
,设
为实数.
,且
,若
,求
的取值范围
设各项均为正数的数列
的前
项和为
,已知
,数列
是公差为
的等差数列.
①求数列
的通项公式(用
表示)
②设
为实数,对满足
且
的任意正整数
,不等式
都成立。求证:
的最大值为
在平面直角坐标系 中,如图,已知椭圆 的左右顶点为 ,右顶点为 ,设过点 的直线 与椭圆分别交于点 , ,其中 ,
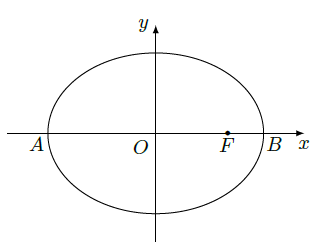
①设动点
满足
,求点
的轨迹
②设
,求点
的坐标
③设
,求证:直线
必过
轴上的一定点(其坐标与
无关)
某兴趣小组测量电视塔 的高度 (单位 ),如示意图,垂直放置的标杆 高度 ,仰角 .
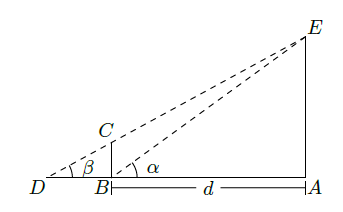
(1)该小组已经测得一组
的值,
,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离
(单位
),使
与
之差较大,可以提高测量精确度,若电视塔实际高度为125
,问
为多少时,
最大.