在 中,角A,B,C所对应的边分别为
中,角A,B,C所对应的边分别为
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值.
的最大值. 
如图,在四棱锥 中,底面ABCD是菱形,
中,底面ABCD是菱形, ,侧面
,侧面 底面ABCD,并且
底面ABCD,并且 ,F为SD的中点.
,F为SD的中点.
(1)求三棱锥 的体积;
的体积;
(2)求直线BD与平面FAC所成角的正弦值.
某学生参加3个项目的体能测试,若该生第一个项目测试过关的概率为 ,第二个项目、第三个项目测试过关的概率分别为x,y(
,第二个项目、第三个项目测试过关的概率分别为x,y( ),且不同项目是否能够测试过关相互独立,记
),且不同项目是否能够测试过关相互独立,记 为该生测试过关的项目数,其分布列如下表所示:
为该生测试过关的项目数,其分布列如下表所示:
(1)求该生至少有2个项目测试过关的概率;
(2)求 的数学期望
的数学期望 .
.
已知向量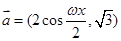 ,
,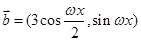 ,
,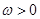 ,设函数
,设函数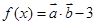 的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且
的部分图象如图所示,A为图象的最低点,B,C为图象与x轴的交点,且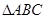 为等边三角形,其高为
为等边三角形,其高为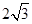 .
.
(1)求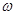 的值及函数
的值及函数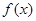 的值域;
的值域;
(2)若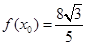 ,且
,且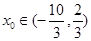 ,求
,求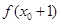 的值.
的值.
已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆 于
于 ,
, 两点,连接
两点,连接 ,
, 分别交直线
分别交直线 于
于 ,
, 两点,若直线
两点,若直线 、
、 的斜率分别为
的斜率分别为 、
、 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
如图,四边形 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.