在棱长为2的正方体ABCD—A1B1C1D1中,E,F分别为A1D1和CC1的中点.
(Ⅰ)求证:EF//平面ACD1;
(Ⅱ)求异面直线EF与AB所成的角的余弦值;
(Ⅲ)在棱BB1上是否存在一点P,使得二面角P—AC—B的大小为30°?若存在,求出BP的长;若不存在,请说明理由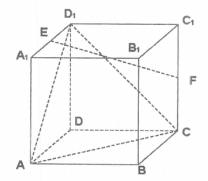
双曲线 ,圆 在第一象限交点为A, ,曲线 。
(1)若 ,求b;
(2)若 , 与x轴交点记为 ,P是曲线 上一点,且在第一象限,并满足 ,求∠ ;
(3)过点 且斜率为 的直线 交曲线 于M、N两点,用b的代数式表示 ,并求出 的取值范围。

已知: , ,且 ,
(1)若v>95,求x的取值范围;
(2)已知x=80时,v=50,求x为多少时,q可以取得最大值,并求出该最大值。
已知 .
(1)若f(x)的周期是4π,求 ,并求此时 的解集;
(2)已知 , , ,求g(x)的值域.
已知边长为1的正方形ABCD,沿BC旋转一周得到圆柱体。
(1)求圆柱体的表面积;
(2)正方形ABCD绕BC逆时针旋转 到 ,求 与平面ABCD所成的角。

已知数集 具有性质 ;对任意的 , 与 两数中至少有一个属于 。
(Ⅰ)分别判断数集 与 是否具有性质 ,并说明理由;
(Ⅱ)证明: ,且
(Ⅲ)证明:当 时, 成等比数列。