在对人们饮食习惯的一次调查中，共调查了124人，其中六十岁以上的70人，六十岁以下的54人，六十岁以上的人中有43人的饮食以蔬菜为主，另外27人则以肉类为主；六十岁以下的人中有21人饮食以蔬菜为主，另外33人则以肉类为主．(1)根据以上数据建立一个2×2的列联表；(2)判断人的饮食习惯是否与年龄有关．
附：“X与Y有关系”的可信程度表：
| P(K2≥k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.01 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.874 |
5.024 |
6.635 |
7.879 |
10.828 |
如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.
(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A
CDF的体积有最大值?并求出这个最大值.
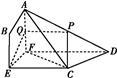
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.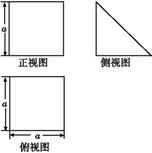
(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
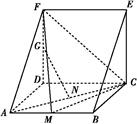
如图所示,四棱锥E
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.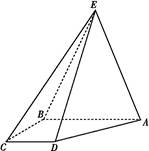
(1)求证:AB⊥ED;
(2)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出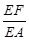
;若不存在,说明理由.
如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=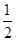
EF=2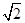
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.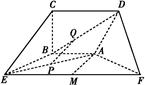
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
如图,四棱锥S
ABCD的底面是正方形,每条侧棱的长都是底面边长的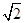
倍,P为侧棱SD上的点.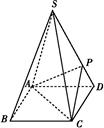
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角PACD的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.