(本小题满分12分)已知 三点的坐标分别是
三点的坐标分别是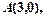
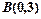 ,
, ,其中
,其中 ,且
,且 .
.
(Ⅰ)求角 的值;(Ⅱ)当
的值;(Ⅱ)当 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
学校餐厅每天供应500名学生用餐,每星期一有A, B两种菜可供选择。调查表明,凡是在这星期一选A菜的,下星期一会有 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第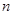 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.
⑴试用 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由;
⑵若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.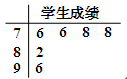
⑴求这6位同学成绩的平均数和标准差;
⑵从这6位同学中随机选出两位同学来分析成绩的分布情况,设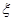 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求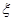 的分布列和期望.
的分布列和期望.
已知点 在双曲线
在双曲线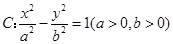 上,且双曲线的一条渐近线的方程是
上,且双曲线的一条渐近线的方程是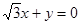 .
.
(1)求双曲线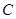 的方程;
的方程;
(2)若过点 且斜率为
且斜率为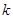 的直线
的直线 与双曲线
与双曲线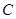 有两个不同交点,求实数
有两个不同交点,求实数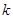 的取值范围;
的取值范围;
(3)设(2)中直线 与双曲线
与双曲线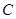 交于
交于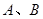 两个不同点,若以线段
两个不同点,若以线段 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数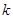 的值.
的值.
已知数列 满足
满足 (
( ).
).
(1)求 的值;
的值;
(2)求 (用含
(用含 的式子表示);
的式子表示);
(3)记 ,数列
,数列
 的前
的前 项和为
项和为 ,求
,求 (用含
(用含 的式子表示).).
的式子表示).).
某通讯公司需要在三角形地带 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域 内.分界线
内.分界线 固定,且
固定,且 =
= 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
.
设 (
( )百米,
)百米, 百米.
百米.
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.