求圆心为(2,1),且与已知圆x2+y2-3x=0的公共弦所在直线过点(5,-2)
的圆的方程.
求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0的交点的圆的方程.
已知一圆过A(4,-2)、B(-1,3)两点,且在y轴上截得的线段长为4 ,求圆的方程.
,求圆的方程.
过圆x2+y2=4外一点A(4,0),作圆的割线,求割线被圆截得的弦的中点的轨迹方程.
已知椭圆的中心在原点,焦点在x轴上,一个顶点A(0,-1),且右焦点到右准线的距离为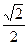 .
.
(1)求椭圆的方程.
(2)试问是否能找到一条斜率为k(k≠0)的直线l,使l与椭圆交于不同两点M、N且满足|AM|=|AN|?若这样的直线存在,求出k的取值范围;若不存在,请说明理由.