设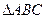 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为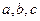 ,且
,且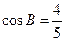 ,
,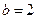 。
。
(1)当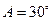 时,求
时,求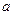 的值.
的值.
(2)当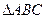 的面积为3时,求
的面积为3时,求 的值.
的值.
在四棱锥P—ABCD中,侧棱PA⊥底面ABCD,底面ABCD是矩形,问底面的边BC上是否存在点E.
(1)使∠PED=90°;
(2)使∠PED为锐角. 证明你的结论.
假设每一架飞机引擎在飞行中故障率为1–p,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行,则对于多大的p而言,4引擎飞机比2引擎飞机更为安全?
如图,三条直线a、b、c两两平行,直线a、b间的距离为p,直线b、c间的距离为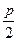 ,A、B为直线a上两定点,且|AB|=2p,MN是在直线b上滑动的长度为2p的线段。
,A、B为直线a上两定点,且|AB|=2p,MN是在直线b上滑动的长度为2p的线段。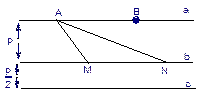
(1)建立适当的平面直角坐标系,求△AMN的外心C的轨迹E;
(2)接上问,当△AMN的外心C在E上什么位置时,d+|BC|最小,最小值是多少?(其中d是外心C到直线c的距离).
已知函数
的图象在与
轴交点处的切线方程是
.
(I)求函数
的解析式;
(II)设函数
,若
的极值存在,求实数
的取值范围以及函数
取得极值时对应的自变量
的值.
设A、B是双曲线x2– =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.
(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?