已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0, )和
)和 (m-b,m2-mb+n),其中a,b,c
(m-b,m2-mb+n),其中a,b,c ,m,n为实数,且a,m不为0.
,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.
如图,在矩形 中,点 为坐标原点,点 的坐标为 ,点 、 在坐标轴上,点 在 边上,直线 ,直线 .
(1)分别求直线 与 轴,直线 与 的交点坐标;
(2)已知点 在第一象限,且是直线 上的点,若 是等腰直角三角形,求点 的坐标;
(3)我们把直线 和直线 上的点所组成的图形为图形 .已知矩形 的顶点 在图形 上, 是坐标平面内的点,且 点的横坐标为 ,请直接写出 的取值范围(不用说明理由).

对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点 的斜平移,如点 经1次斜平移后的点的坐标为 ,已知点 的坐标为 .
(1)分别写出点 经1次,2次斜平移后得到的点的坐标.
(2)如图,点 是直线 上的一点,点 关于点 的对称点为点 ,点 关于直线 的对称点为点 .
①若 、 、 三点不在同一条直线上,判断 是否是直角三角形?请说明理由.
②若点 由点 经 次斜平移后得到,且点 的坐标为 ,求出点 的坐标及 的值.

如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条 , , 不动, , ,如图,量得第四根木条 ,判断此时 与 是否相等,并说明理由.
(2)若固定二根木条 、 不动, , ,量得木条 , ,写出木条 的长度可能取得的一个值(直接写出一个即可)
(3)若固定一根木条 不动, ,量得木条 ,如果木条 , 的长度不变,当点 移到 的延长线上时,点 也在 的延长线上;当点 移到 的延长线上时,点 、 、 能构成周长为 的三角形,求出木条 , 的长度.

课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为 ,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为 时,透光面积最大值约为 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为 ,利用图3,解答下列问题:
(1)若 为 ,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.

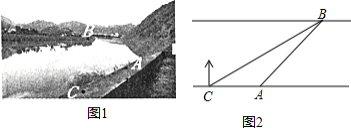
如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点 处,测得河的北岸边点 在其北偏东 方向,然后向西走 到达 点,测得点 在点 的北偏东 方向,如图2.
(1)求 的度数.
(2)求出这段河的宽(结果精确到 ,备用数据 , .