(本小题满分13分)
已知点 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点 到直线
到直线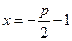 (
(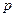 是正常数)的距离为
是正常数)的距离为 ,到点
,到点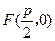 的距离为
的距离为 ,且
,且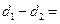 1.
1.
(1)求动点P所在曲线C的方程;
(2)直线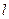 过点F且与曲线C交于不同两点A、B,分别过A、B点作直线
过点F且与曲线C交于不同两点A、B,分别过A、B点作直线 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为 ,求证
,求证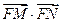 =
=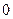 ;
;
(3)记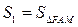 ,
, ,
,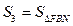 (A、B、
(A、B、 是(2)中的点),
是(2)中的点),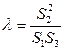 ,求
,求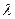 的值.
的值.
已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值及抛物线E2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
 ,
, ,
, .
.
特例探索
(1)如图1,当∠ =45°,
=45°, 时,
时, = ,
= , ;
;
如图2,当∠ =30°,
=30°, 时,
时, = ,
= , ;
;
归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=  ,AB=3.求AF的长.
,AB=3.求AF的长.
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
(1)求证:PA是⊙O的切线;
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为 的中点,且∠DCF=∠P,求证:
的中点,且∠DCF=∠P,求证: .
.
如图,已知直线 与双曲线
与双曲线 交于A(
交于A( ),B(
),B( )两点(A与B不重合),直线AB与
)两点(A与B不重合),直线AB与 轴交于P(
轴交于P( ),与
),与 轴交于点C.
轴交于点C.
(1)若A,B两点的坐标分别为(1,3),(3,y2).求点P的坐标;
(2)若 ,点
,点 的坐标为(6,0),且
的坐标为(6,0),且 .求
.求 两点的坐标;
两点的坐标;
(3)结合(1),(2)中的结果,猜想并用等式表示 之间的关系(不要求证明).
之间的关系(不要求证明).
已知关于x的方程x2+2x+a﹣2=0
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)若该方程的一个根为1,求a的值及该方程的另一根.