(本小题满分12分)已知各项均为正数的数列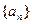 的前
的前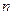 项和
项和 满足
满足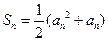
(1)求 的值; (2)求
的值; (2)求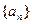 的通项公式;
的通项公式;
(3)是否存在正数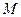 使下列不等式:
使下列不等式: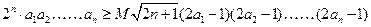
对一切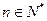 成立?若存在,求出M的取值范围;若不存在,请说明理由
成立?若存在,求出M的取值范围;若不存在,请说明理由
(本小题满分13分)设函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)当 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
(本小题满分13分)已知集合 ,
, .
.
(1)当 时,求
时,求 ;(2)若
;(2)若 ,求实数
,求实数 的值.
的值.
(本题 10分)定义在R上的函数
10分)定义在R上的函数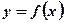 ,对任意的
,对任意的 ,满足
,满足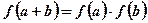 ,当
,当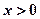 时,有
时,有 ,其中
,其中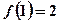 .
.
(1)求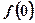 的值;
的值;
(2)求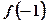 的值并判断该函数的奇偶性;
的值并判断该函数的奇偶性;
(3)求不等式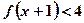 的解集.
的解集.
(本题10 分)某市居民自
分)某市居民自 来水收费标准如下:每月用水不超过
来水收费标准如下:每月用水不超过 时每吨
时每吨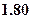 元,当用水超过
元,当用水超过 时,超过部分每吨
时,超过部分每吨 元,某月
元,某月 甲、乙两户共交水费
甲、乙两户共交水费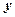
 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为 ,
, 。
。
(1)求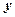 关于
关于 的函数;
的函数;
(2)若甲、乙两户该月共交水费 元,分别求出甲、乙两户该月的用水量和水费。
元,分别求出甲、乙两户该月的用水量和水费。
(本题10分)
已知函数 (
( ∈R).
∈R).
(1)试给出 的一个值,并画出此时函数的图象;
的一个值,并画出此时函数的图象;
(2)若函数f (x)在 R 上具有单调性,求 的取值范围.
的取值范围.