(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
,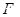 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点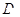 到平面
到平面 的距离.
的距离.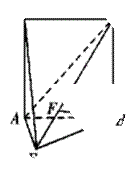
证明不等式:
已知函数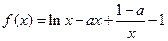
 .
.
(Ⅰ)当 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅱ)设 当
当 时,若对任意
时,若对任意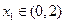 ,存在
,存在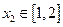 ,使
,使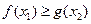 ,求实数
,求实数 取值范围.
取值范围.
如图,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为
 .一等轴双曲线的顶
.一等轴双曲线的顶 点是该椭圆的焦点,设
点是该椭圆的焦点,设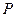 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和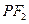 与椭圆的交点分别为
与椭圆的交点分别为 和
和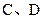 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线 、
、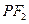 的斜率分别为
的斜率分别为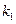 、
、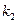 ,证明
,证明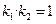 ;
;
(Ⅲ)是否存在常数 ,使得
,使得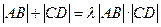 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某学校举行知识竞赛,第一轮选拔共设有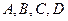 四个问题,规则如下:
四个问题,规则如下:
①每位参加者计分器的初始分均为10分,答对问题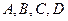 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;
②每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局,当累计分数大于或等于14分时,答题结束 ,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③每位参加者按问题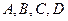 顺序作答,直至答题结束.
顺序作答,直至答题结束.
假设甲同学对问题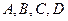 回答正确的概率依次为
回答正确的概率依次为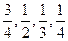 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用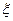 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求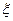 的分布列和数学的
的分布列和数学的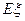 .
.
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, ABC=45°,AB=2
ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.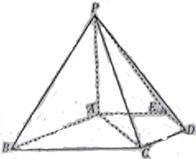
(Ⅰ)求证 :平面PCD⊥平面PAC;
:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥 P—ACDE的体积.
P—ACDE的体积.