养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M,高4M。养路处拟建一个 更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是
更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是 高度增加4M(底面直径不变)。
高度增加4M(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些,说明理由.
(本小题共14分)
设函数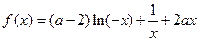 (
(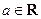 ).
).
(Ⅰ)当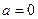 时,求
时,求 的极值;
的极值;
(Ⅱ)当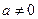 时,求
时,求 的单调区间.
的单调区间.
( 本小题共13分)
本小题共13分)
某学校高一年级开设了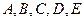 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量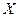 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加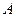 课程的人数,求
课程的人数,求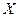 的分布列与数学期望.
的分布列与数学期望.
(本小题共14分)
正方体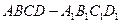 的棱长为
的棱长为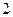 ,
,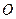 是
是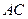 与
与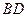 的交点,
的交点,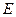 是
是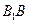 上一点,且
上一点,且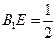 .(Ⅰ)求证:
.(Ⅰ)求证: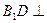 平面
平面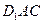 ;
;
(Ⅱ)求异面直线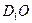 与
与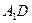 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线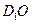 与平面
与平面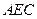 所成角的正弦值.
所成角的正弦值.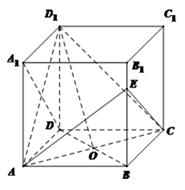
(本小题共12分)
|
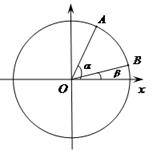
如图,在平面直角坐标系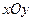 中,以
中,以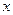 轴为始边作两个锐角
轴为始边作两个锐角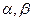 ,它们的终边分别与单位圆交于
,它们的终边分别与单位圆交于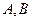 两点.已知
两点.已知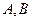 的横坐标分别为
的横坐标分别为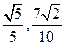 .
.
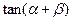 的值;
的值;
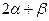 的值.
的值.
设不等式组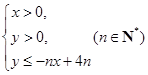 ,所表示的平面区域
,所表示的平面区域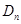 的整点个数为
的整点个数为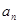 ,则
,则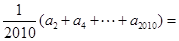 .
.