设
均为正数,且
,证明:
(Ⅰ)若
,则
;
(Ⅱ)
是
的充要条件.
在直角坐标系
中,曲线
(
为参数,
),其中
,在以
为极点,
轴正半轴为极轴的极坐标系中,曲线
,曲线
.
(Ⅰ)求
与
交点的直角坐标;
(Ⅱ)若
与
相交于点
,
与
相交于点
,求
的最大值.
选修4-1:几何证明选讲
如图,
为等腰三角形
内一点,圆
与
的底边
交于
、
两点与底边上的高
交于点
,与
、
分别相切于
、
两点.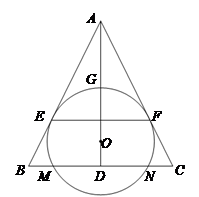
(Ⅰ)证明:
;
(Ⅱ) 若
等于
的半径,且
,求四边形
的面积.
设函数
.
(Ⅰ)证明:
在
单调递减,在
单调递增;
(Ⅱ)若对于任意
,都有
,求
的取值范围.
已知椭圆
,直线
不过原点
且不平行于坐标轴,
与
有两个交点
,线段
的中点为
.
(Ⅰ)证明:直线
的斜率与
的斜率的乘积为定值;
(Ⅱ)若
过点
,延长线段
与
交于点
,四边形
能否为平行四边形?若能,求此时
的斜率,若不能,说明理由.