(本小题满分12分)某校从参加高二级期中考试的学生中抽出60名学生,将其成绩(均为整数)分成六段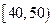 ,
,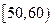 ,…,
,…,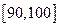 .后画出如下部分频率分布直方图.观察图形的信息,回答下列题:
.后画出如下部分频率分布直方图.观察图形的信息,回答下列题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分以上为及格);若统计方法中,同一组数据用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)从成绩是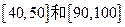 分的学生中选两人,求他们在同一分数段的概率.
分的学生中选两人,求他们在同一分数段的概率.
已知不等式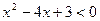 的解集是
的解集是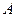 .
.
(Ⅰ)求集合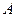 ;
;
(Ⅱ)函数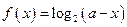
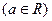 的定义域为集合
的定义域为集合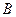 ,若
,若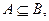
 求
求 的取值范围;
的取值范围;
(Ⅲ)不等式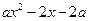
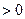
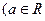 且
且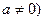 的解集为
的解集为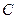 ,若
,若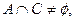 求
求 的取
的取 值范围.
值范围.
设等差数列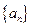
 的前
的前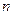 项和为
项和为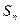 ,等比数列
,等比数列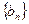 的前
的前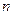 项和为
项和为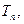 已知数列
已知数列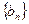 的公比
的公比
为
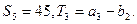
(Ⅰ )求数列
)求数列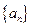 ,
,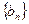 的通项公式;
的通项公式;
(Ⅱ)求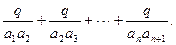

如图四边形 是菱形,
是菱形, 平面
平面 ,
,
 为
为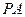 的中点.
的中点.
求证:(Ⅰ)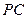 ∥平
∥平 面
面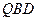 ;
;
(Ⅱ)平面 平面
平面
已知圆 过点
过点 、
、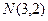 ,
, 且圆心在直线
且圆心在直线 上.
上.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)求圆 过点
过点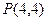 的最短弦所在的直线方程.
的最短弦所在的直线方程.
(本题满分12分)汽车行业是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取 辆进行
辆进行 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
 |
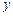 |
160 |
经测算发现,乙品牌车 排放量的平
排放量的平 均值为
均值为
 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 排放量的稳定性.
排放量的稳定性.