已知:函数
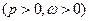 的最大值为
的最大值为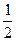 ,最小正周期为
,最小正周期为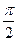 .
.
(Ⅰ)求: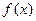 的解析式;
的解析式;
(Ⅱ)若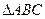 的三条边为
的三条边为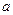 ,
,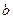 ,
,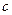 ,满足
,满足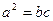 ,
,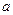 边所对的角为
边所对的角为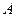 .求:角
.求:角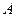 的取值范围及函数
的取值范围及函数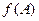 的值域.
的值域.
已知集合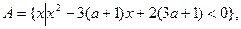
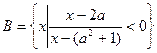 ,
,
(Ⅰ)当 时,求
时,求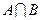 ;
;
(Ⅱ)求使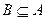 的实数
的实数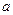 的取值范围。
的取值范围。
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点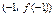 处的切线的斜率是
处的切线的斜率是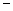 5.
5.
(1)求实数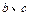 的值;
的值;
(2)求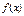 在区间
在区间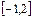 上的最大值;
上的最大值;
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA="AD=1,AB=2," 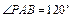 ,
,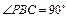 .
.
(1)求证:平面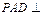 平面
平面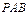 ;
;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.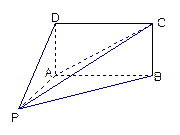
锐角三角形ABC的三内角A、B、C所对边的长分别为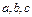 ,设向量
,设向量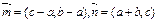 ,且
,且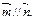
(1)求角B的大小;
(2)若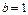 ,求
,求 的取值范围。
的取值范围。