已知
,求
的值.
如图为了确定各建筑物的位置：（1）以火车站为原点建立直角坐标系．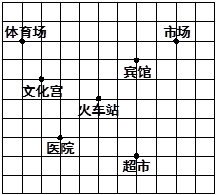
（2）写出市场、超市的坐标.
、
（3）请将体育场、宾馆和火车站看作三点用线段连起来，得△ABC，然后将此三角形向下平移4 个单位长度,再画出平移后的△A/B/C/.
（4）△ABC的面积是_________
如图，已知直角梯形ABCD中，AD∥BC，AB⊥BC ，AD＝2cm，AB＝8cm，CD＝10cm．
(1)求梯形ABCD的周长；
(2)动点P从点B出发，以1cm/s的速度沿B→A→D→C方向向点C运动；动点Q从点C出发，以1cm/s的速度沿C→D→A方向向点A运动；过点Q作QF⊥BC于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之结束，设运动时间为t秒．问：
在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．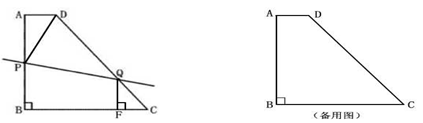
如图，将边长为3cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD的中点 M处，点C落在点N处，MN与CD交于点P， 连接EP．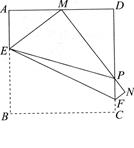
(1) △AEM的周长=_____cm；（2）求证：EP=AE+DP；
在国家政策的宏观调控下，某地区的商品房成交价由今年3月份的15000元/
下降到5月份的12150元/.
⑴求4、5两月平均每月降价的百分率是多少？
⑵如果房价继续回落，按此降价的百分率，你预测到6月份该地区的商品房成交均价是否会跌破10000元/？请说明理由.
阅读下面的材料，并解答问题：
材料：已知当a、b是正数时，有下列命题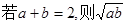
≤1
≤
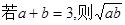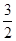
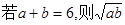≤ 3
（1）根据以上三个命题所提供的规律猜想：
≤ ；
（2）以上规律可用字母表示为 ；
（3）建造一个容积为8立方米，深2米的长方形无盖水池，池底和池壁的造价分别为每平方米120元和80元.设池底的长为x米，水池总造价为y元，应用上述的规律，求水池的最低造价.