某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水池的长和宽,使总造价最低.
已知函数 ,其中a为实数。
,其中a为实数。
(1)求函数 的单调区间;
的单调区间;
(2)若函数 对定义域内的任意x恒成立,求实数a的取值范围。
对定义域内的任意x恒成立,求实数a的取值范围。
(3)证明,对于任意的正整数m,n,不等式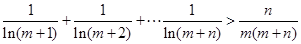 恒成立。
恒成立。
已知函数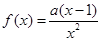 ,其中
,其中 。
。
(1)若直线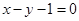 是曲线
是曲线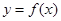 的切线,求a的值;
的切线,求a的值;
(2)设 ,求
,求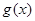 在区间
在区间 上的最大值。(其中e为自然对数的底数)。
上的最大值。(其中e为自然对数的底数)。
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计)。有人应用数学知识作如下设计:在钢板的四个角处各切去一个全等的小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长。
(1)请你求出这种切割、焊接而成的长方体容器的最大容积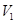 ;
;
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积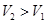 。
。
设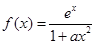 ,其中a为正实数。
,其中a为正实数。
(1)当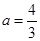 时,求
时,求 的极值点;
的极值点;
(2)若 在R不是单调函数,求a的取值范围。
在R不是单调函数,求a的取值范围。
已知数列 满足
满足 ,且
,且 。
。
(1)求 。
。
(2)猜想数列 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。