如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求EF和平面ABCD所成的角α的正切;
(Ⅲ)求异面直线EF与BD所成的角β的余弦.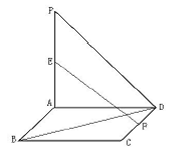
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
(1)请根据频率分布直方图,估算样本数据的众数和中位数(中位数精确到0.01);
(2)若将频率视为概率,从该生产线所生产的产品(数量很多)中随机抽取3个,用ξ表示连续使用寿命高于350天的产品件数,求ξ的分布列和期望.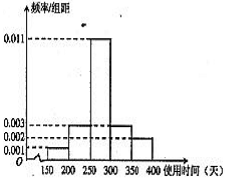
已知向量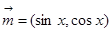 ,
, ,函数
,函数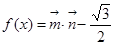 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)如果△ABC的三边 所对的角分别为
所对的角分别为 、
、 、
、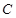 ,且满足
,且满足 ,求
,求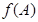 的值.
的值.
已知数列 的前
的前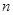 项和为
项和为 ,常数
,常数 ,且
,且 对一切正整数
对一切正整数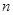 都成立。
都成立。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设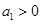 ,
, ,求证:
,求证: 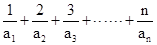 <4.
<4.
在△ABC中,a, b, c分别为内角A, B, C的对边,且满足
2asinA=(2b+c)sinB+(2c+b)sinC
(Ⅰ)求A的大小;
(Ⅱ)求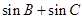 的最大值.
的最大值.