(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为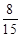 ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为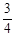 ,每个男生通过的概率均为
,每个男生通过的概率均为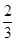 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ)若 ,且
,且 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(Ⅱ)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 、
、 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,是否存在点
,是否存在点 ,使
,使 在点
在点 处的切线与
处的切线与 在点
在点 处的切线平行?如果存在,求出点
处的切线平行?如果存在,求出点 的横坐标,如果不存在,说明理由.
的横坐标,如果不存在,说明理由.
(本小题满分12分)已知椭圆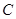 :
: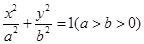 的焦点分别为
的焦点分别为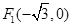 、
、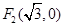 ,点
,点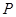 在椭圆
在椭圆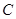 上,满足
上,满足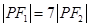 ,
,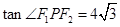 .
.
(Ⅰ)求椭圆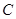 的方程;
的方程;
(Ⅱ)已知点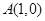 ,试探究是否存在直线
,试探究是否存在直线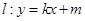 与椭圆
与椭圆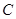 交于
交于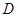 、
、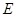 两点,且使得
两点,且使得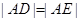 ?若存在,求出
?若存在,求出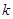 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)如图,在三棱柱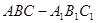 中,面
中,面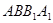 为矩形,
为矩形,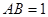 ,
,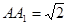 ,
,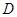 为
为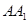 的中点,
的中点,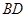 与
与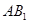 交于点
交于点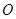 ,
,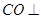 面
面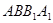 .
.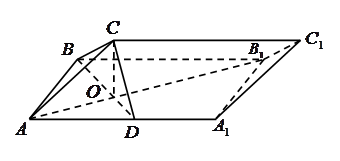
(Ⅰ)证明: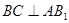 ;
;
(Ⅱ)若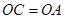 ,求二面角
,求二面角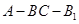 的余弦值.
的余弦值.
(本小题满分12分)某企业有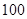 位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有
位员工.拟在新年联欢会中,增加一个摸球兑奖的环节,规定:每位员工从一个装有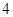 个标有面值的球的袋中一次性随机摸出
个标有面值的球的袋中一次性随机摸出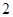 个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为
个球,球上所标的面值之和为该员工所获的中奖额.企业预算抽奖总额为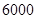 元,共提出两种方案.
元,共提出两种方案.
方案一:袋中所装的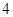 个球中有两个球所标的面值为
个球中有两个球所标的面值为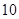 元,另外两个标的面值为
元,另外两个标的面值为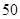 元;
元;
方案二:袋中所装的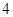 个球中有两个球所标的面值为
个球中有两个球所标的面值为 元,另外两个标的面值为
元,另外两个标的面值为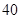 元.
元.
(Ⅰ)求两种方案中,某员工获奖金额的分布列;
(Ⅱ)在两种方案中,请帮助该企业选择一个适合的方案,并说明理由.
(本小题满分12分)已知函数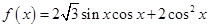
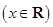 .
.
(Ⅰ)求函数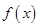 的最小正周期及在区间
的最小正周期及在区间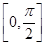 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)将函数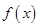 图像向左平移
图像向左平移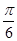 个单位,再向上平移
个单位,再向上平移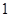 个单位,得到函数
个单位,得到函数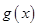 图像,求
图像,求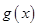 的对称轴方程和对称中心坐标.
的对称轴方程和对称中心坐标.