(本题满分15分) 已知函数f (x)=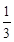 x3+ax2+bx, a , b
x3+ax2+bx, a , b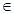 R.
R.
(Ⅰ) 曲线C:y=f (x) 经过点P (1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f (x )在区间 (1,2) 内存在两个极值点,求证:0<a+b<2.
)在区间 (1,2) 内存在两个极值点,求证:0<a+b<2.
已知函数 时,
时, 的值域为
的值域为 ,当
,当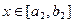
时, 的值域为
的值域为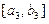 ,依次类推,一般地,当
,依次类推,一般地,当 时,
时, 的值域为
的值域为 ,其中k、m为常数,且
,其中k、m为常数,且
(1)若k=1,求数列 的通项公式;
的通项公式;
(2)项m=2,问是否存在常数 ,使得数列
,使得数列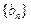 满足
满足 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;
(3)若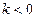 ,设数列
,设数列 的前n项和分别为Sn,Tn,求
的前n项和分别为Sn,Tn,求 。
。
已知函数 ,其中a为常数,且
,其中a为常数,且
(1)若 是奇函数,求a的取值集合A;
是奇函数,求a的取值集合A;
(2)当a=-1时,设 的反函数为
的反函数为 ,且函数
,且函数 的图像与
的图像与 的图像关于
的图像关于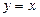 对称,求
对称,求 的取值集合B。
的取值集合B。
(3)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式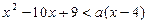 恒成立,求x的取值范围。
恒成立,求x的取值范围。
数列 满足
满足 ,
, .
.
(1)求 通项公式
通项公式 ;
;
(2)令 ,数列
,数列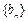 前
前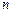 项和为
项和为 ,
,
求证:当 时,
时, ;
;
(3)证明: .
.
已知数列 中,
中, ,对于任意的
,对于任意的 ,有
,有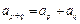
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足:
满足: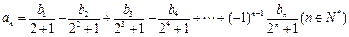 求数列
求数列 的通项公式;
的通项公式;
(3)设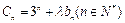 ,是否存在实数
,是否存在实数 ,当
,当 时,
时,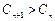 恒成立,若存在,求实数
恒成立,若存在,求实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
已知 各项均为正数的数列
各项均为正数的数列 满足
满足 ,
, ,
,  .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)当 取何值时,
取何值时, 取最大值,并求出最大值;
取最大值,并求出最大值;
(Ⅲ)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.