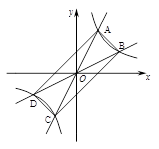
如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=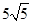 ,且
,且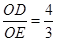 ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l: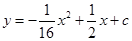 经过点E,且与AB边相交于点F.
经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.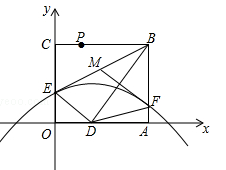
如图,在平面直角坐标系中,⊙A与x轴相交于C(﹣2,0),D(﹣8,0)两点,与y轴相切于点B(0,4).
(1)求经过B,C,D三点的抛物线的函数表达式;
(2)设抛物线的顶点为E,求证:直线CE与⊙A相切;
(3)在x轴下方的抛物线上,是否存在一点F,使△BDF面积最大,最大值是多少?并求出点F的坐标.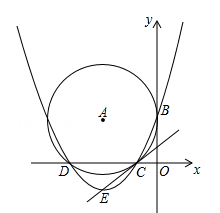
(为方便答题,可在答题卡上画出你认为必要的图形)
如图,过原点的直线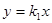 和
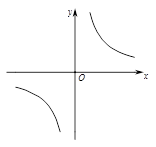
和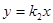 与反比例函数
与反比例函数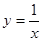 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由;
(3)设P(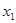 ,
,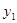 ),Q(
),Q(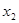 ,
,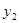 )(x2 > x1 > 0)是函数
)(x2 > x1 > 0)是函数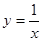 图象上的任意两点,
图象上的任意两点,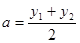 ,
,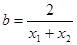 ,试判断
,试判断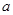 ,
,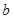 的大小关系,并说明理由.
的大小关系,并说明理由.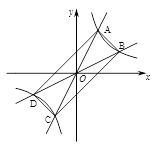

已知O为坐标原点,抛物线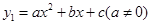 与
与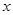 轴相交于点
轴相交于点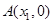 ,
,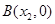 .与
.与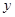 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,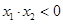 ,
,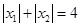 ,点A,C在直线
,点A,C在直线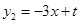 上.
上.
(1)求点C的坐标;
(2)当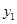 随着
随着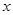 的增大而增大时,求自变量
的增大而增大时,求自变量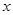 的取值范围;
的取值范围;
(3)将抛物线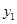 向左平移
向左平移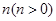 个单位,记平移后
个单位,记平移后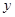 随着
随着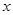 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线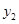 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求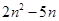 的最小值.
的最小值.
如图,过原点的直线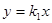 和
和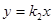 与反比例函数
与反比例函数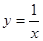 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时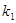 和
和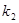 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(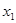 ,
,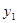 ),Q(
),Q(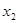 ,
,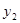 )(
)(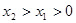 )是函数
)是函数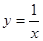 图象上的任意两点,
图象上的任意两点,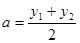 ,
,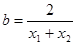 ,试判断
,试判断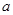 ,
,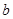 的大小关系,并说明理由.
的大小关系,并说明理由.