设函数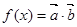 ,其中向量
,其中向量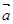 =(2cosx,1),
=(2cosx,1),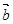 =(cosx,
=(cosx, sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- 且x∈[-
且x∈[-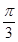 ,
,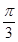 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量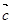 =(m,n)(|m|<
=(m,n)(|m|<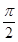 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
某中学调查了某班全部  名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)

(1)从该班随机选  名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的  名同学中,有5名男同学
名同学中,有5名男同学
 名女同学
现从这
名女同学
现从这  名男同学和
名男同学和  名女同学中各随机选
名女同学中各随机选  人,求
被选中且
未被选中的概率.
人,求
被选中且
未被选中的概率.
设函数
,其中
.
(Ⅰ)讨论函数
极值点的个数,并说明理由;
(Ⅱ)若
成立,求
的取值范围.
平面直角坐标系
中,已知椭圆
的离心率为
,左、右焦点分别是
,以
为圆心以3为半径的圆与以
为圆心以1为半径的圆相交,且交点在椭圆
上.
(Ⅰ)求椭圆
的方程;
(Ⅱ)设椭圆
,
为椭圆
上任意一点,过点
的直线
交椭圆
于
两点,射线
交椭圆
于点
.
(i)求
的值;
(Ⅱ)求
面积的最大值.
若
是一个三位正整数,且
的个位数字大于十位数字,十位数字大于百位数字,则称
为"三位递增数"(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的"三位递增数"中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的"三位递增数"的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的"三位递增数" ;
(Ⅱ)若甲参加活动,求甲得分
的分布列和数学期望
.
设数列
的前
项和为
.已知
.
(Ⅰ)求
的通项公式;
(Ⅱ)若数列
满足
,求
的前
项和
.