一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,现从袋中每次任取一球,每次取出不放回,连续取两次,问:
(1)取出的两只球都是白球的概率是多少;
(2)取出的两球至少有一个白球的概率是多少。
已知二次函数f(x)满足条件f(0)=1和f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值.
求值:
(1)已知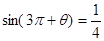 ,
,
求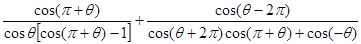 的值;
的值;
(2)已知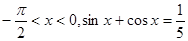 ,求
,求 的值。
的值。
已知二次函数 的导函数的图像与直线
的导函数的图像与直线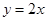 平行,且
平行,且 在
在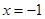 处取得极小值
处取得极小值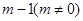 .设
.设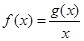 .
.
(1)若曲线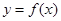 上的点
上的点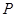 到点
到点 的距离的最小值为
的距离的最小值为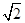 ,求
,求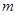 的值;
的值;
(2)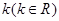 如何取值时,函数
如何取值时,函数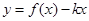 存在零点,并求出零点.
存在零点,并求出零点.
定义:设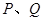 分别为曲线
分别为曲线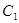 和
和 上的点,把
上的点,把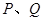 两点距离的最小值称为曲线
两点距离的最小值称为曲线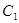 到
到 的距离.
的距离.
(1)求曲线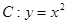 到直线
到直线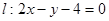 的距离;
的距离;
(2)已知曲线 到直线
到直线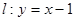 的距离为
的距离为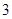 ,求实数
,求实数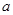 的值;
的值;
(3)求圆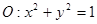 到曲线
到曲线 的距离.
的距离.
设正四棱锥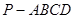 的侧面积为
的侧面积为 ,若
,若 .
.
(1)求四棱锥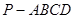 的体积;
的体积;
(2)求直线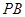 与平面
与平面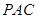 所成角的大小.
所成角的大小.