在平面直角坐标系中，一动点P（
，y）从M（1，0）出发，沿由A（-1，1），B（-1，-1），C（1，-1），D（1，1）四点组成的正方形边线（如图①）按一定方向运动。图②是P点运动的路程s（个单位）与运动时间
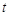（秒）之间的函数图象，图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
（1）求s与
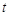之间的函数关系式。（2）求与图③相对应的P点的运动路径；及P点出发多少秒首次到达点B；
（3）写出当3≤s≤8时，y与s之间的函数关系式，并在图③中补全函数图象.
某图书馆开展两种方式的租书业务：一种是使用会员卡，另一种是使用租书卡，使用这两种卡租书，租书金额y(元)琚租书时间x(天)之间的关系如下图所示。
（1）分别求出用租书卡和会员卡租书的金额y(元)琚租书时间x(天)之间的关系式；
（2）两种租书方式每天租书的收费分别是多少元（不含卡费）
（3）若两种租书卡使用期限均为一年（一年按365天计算），则这一年中如何选取这两种租书方式比较合算？
已知函数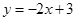
（1）画出这个函数的图象；
（2）写出这个函数的图象与x轴，y轴的交点坐标
（3）求此函数的图象与坐标轴围成的三角形的面积。
已知汽车油箱中有油40升，汽车每行驶1小时消耗5升油，求油箱中的余油量Q（升）与行驶时间t（小时）之间的函数关系，并作出函数的图象。
已知一次函数图象经过点A（2，1）和点（－2，5），求这个一次函数的解析式.
已知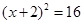
，求
.