(本小题满分12分)
巳知函数
(1) 求. 的值域;
的值域;
(2) 求.. .的单调
.的单调 递增区间.
递增区间.
(本小题满分14分)
已知数列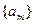 是首项为
是首项为 ,公差为
,公差为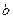 的等差数列,
的等差数列,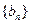 是首项为
是首项为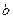 ,公比为
,公比为 的等比数列,且满足
的等比数列,且满足 ,其中
,其中 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列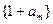 与数列
与数列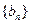 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列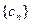 ,求数列
,求数列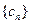 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列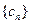 的前项之和为
的前项之和为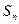 ,求证:
,求证: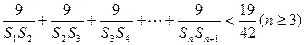 .
.
(本小题满分13分)
已知函数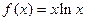
(I)求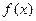 的最小值;
的最小值;
(II)讨论关于x的方程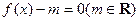 的解的个数;
的解的个数;
(III)当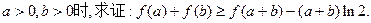
(本小题满分12分)
椭圆C的中心为坐标原点O,焦点在y轴上,短轴长为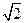 、离心率为
、离心率为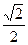 ,直线
,直线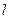 与y轴交于点P(0,
与y轴交于点P(0,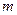 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且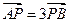 。
。
(I)求椭圆方程;
(II)求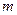 的取值范围。
的取值范围。
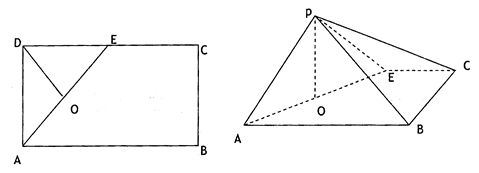
如图所示,在矩形ABCD中,AB=4,AD=2 ,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
(1)求证:PO⊥面ABCE;
(2)求AC与面PAB所成角 的正弦值.
的正弦值.