(本小题满分14分)
已知数列 满足:
满足: ,
,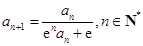 (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求数列 的通项
的通项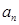 ;
;
(2)设 ,
, ,求证:
,求证: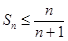 ,
, 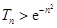 .
.
以直角坐标系的原点为极点O, 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.
已知函数
(1).求函数f(x)的单调区间及极值;
(2).若x1≠x2满足f(x1)=f(x2),求证:x1+x2<0
已知平面上的动点P(x,y)及两个定点A(-2,0),B(2,0),直线PA,PB的斜率分别为K1,K2且K1K2=-
(1).求动点P的轨迹C方程;
(2).设直线L:y=kx+m与曲线C交于不同两点,M,N,当OM⊥ON时,求O点到直线L的距离(O为坐标原点)
如图,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD所在平面垂直于该半圆所在的平面,且AB=2AD=2。
(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积