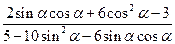已知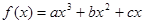 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间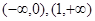 上是减函数,又
上是减函数,又
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
(本小题14分)
如图,已知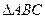 的面积为14,
的面积为14,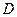 、
、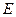 分别为边
分别为边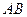 、
、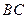 上的点,且
上的点,且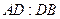
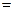
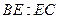
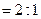 ,
,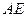 与
与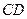 交于
交于 。设存在
。设存在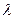 和
和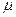 使
使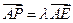 ,
,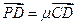 ,
,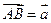 ,
,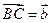 。
。
(1)求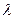 及
及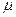
(2)用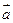 ,
,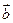 表示
表示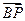
(3)求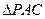 的面积
的面积
(本小题14分)
已知函数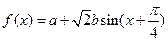 的图象过点(0,1),当
的图象过点(0,1),当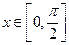 时,
时,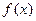 的最大值为
的最大值为 。
。
(1)求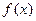 的解析式;
的解析式;
(2)写出由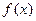 经过平移变换得到的一个奇函数
经过平移变换得到的一个奇函数 的解析式,并说明变化过程
的解析式,并说明变化过程
(本小题14分)
某市的一家报刊摊点,从报社买进《晚报》的价格是每份0.20元,卖出价是每份0.30元,卖不掉的报纸可以以每份0.05元价格退回报社.在一个月(以30天计)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
(本小题12分)
已知 ,
,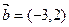 ,当
,当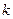 为何值时,
为何值时,
(1) 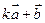 与
与 垂直?
垂直?
(2) 
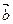 与
与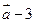
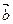 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(本小题12分)
已知 , 计算:
, 计算:
(1) 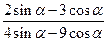 ; (2)
; (2)