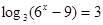(本小题满分15分)
已知抛物线 上任一点到焦点的距离比到y轴距离大1。
上任一点到焦点的距离比到y轴距离大1。
(1)求抛物线的方程;
(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M(4,0),求 的面积的最大值。
的面积的最大值。
(本题共14分)已知函数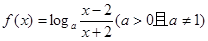 。
。
(1)求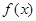 的定义域;
的定义域;
(2)判定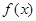 的奇偶性;
的奇偶性;
(3)是否存在实数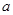 ,使得
,使得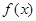 的定义域为
的定义域为 时,值域为
时,值域为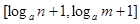 ?若存在,求出实数
?若存在,求出实数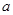 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
(本题共13分)已知函数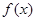 在
在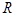 上满足
上满足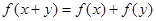 ,且当
,且当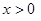 时,
时,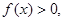
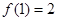 。
。
(1)求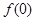 、
、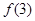 的值;
的值;
(2)判定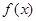 的单调性;
的单调性;
(3)若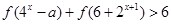 对任意x恒成立,求实数
对任意x恒成立,求实数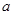 的取值范围。
的取值范围。
(本题共12分)有一小型自来水厂,蓄水池中已有水450吨,水厂每小时可向蓄水池注水80吨,同时蓄水池向居民小区供水,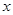 小时内供水总量为
小时内供水总量为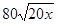 吨。现在开始向池中注水并同时向居民小区供水,问:
吨。现在开始向池中注水并同时向居民小区供水,问:
(1)多少小时后蓄水池中的水量最少?
(2)如果蓄水池中存水量少于150吨时,就会出现供水紧张,那么有几个小时供水紧张?
(本题共12分)设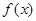 为定义在
为定义在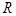 上的偶函数,当
上的偶函数,当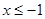 时,
时,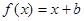 ,且
,且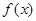 的图象经过点
的图象经过点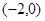 ,又在
,又在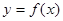 的图象中,有一部分是顶点为(0,2),且过
的图象中,有一部分是顶点为(0,2),且过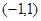 的一段抛物线。
的一段抛物线。
(1)试求出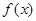 的表达式;
的表达式;
(2)求出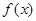 值域;
值域;
(本题共12分)
(1)计算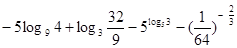
(2)解方程: