某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| |
文艺节目 |
新闻节目 |
总计 |
| 20至40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?(答:“是”或“否”)
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率
(本小题满分10分)选修4-1:几何证明选讲
如图,⊙ 的直径
的直径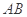 的延长线与弦
的延长线与弦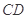 的延长线相交于点
的延长线相交于点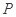 ,
,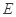 为⊙
为⊙ 上一点,AE=AC ,
上一点,AE=AC ,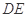 交
交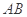 于点
于点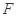 ,且
,且 ,
,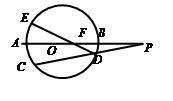
(Ⅰ)求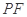 的长度.
的长度.
(Ⅱ)若圆F与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
已知函数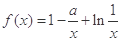 (
( 为实数).
为实数).
(Ⅰ)当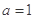 时,求函数
时,求函数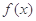 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)设函数 (其中
(其中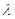 为常数),若函数
为常数),若函数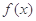 在区间
在区间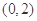 上不存在极值,且存在
上不存在极值,且存在 满足
满足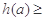
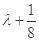 ,求
,求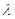 的取值范围;
的取值范围;
(Ⅲ)已知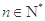 ,求证:
,求证: .
.
设A是圆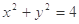 上的任意一点,
上的任意一点,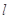 是过点A与
是过点A与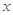 轴垂直的直线,D是直线
轴垂直的直线,D是直线 与
与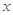 轴的交点,点M在直线
轴的交点,点M在直线 上,且满足
上,且满足 .当点A在圆上运动时,记点M的轨迹为曲线
.当点A在圆上运动时,记点M的轨迹为曲线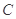 .
.
(1)求曲线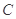 的标准方程;
的标准方程;
(2)设曲线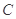 的左右焦点分别为
的左右焦点分别为 、
、 ,经过
,经过 的直线
的直线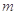 与曲线
与曲线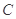 交于P、Q两点,若
交于P、Q两点,若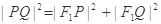 ,求直线
,求直线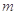 的方程.
的方程.
某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为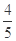 ,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为
,m,n(m>n),设该同学三门课程都取得优秀成绩的概率为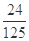 ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为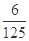 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求m,n;
(2)设X为该同学取得优秀成绩的课程门数,求EX.
如图,已知四棱锥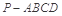 的底面
的底面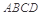 是正方形,侧棱
是正方形,侧棱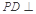 底面
底面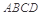 ,
,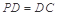 ,
,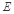 是
是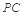 的中点.
的中点.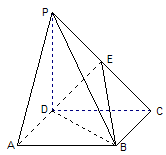
(1)证明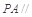 平面
平面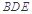 ;
;
(2)求二面角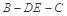 的余弦值.
的余弦值.