某中学从参加高一年级上期期末考试的学生中抽出60名学生，将其-优题课

某中学从参加高一年级上期期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段，…后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）估计这次考试的及格率（60分及以上为及格）；
(Ⅱ) 从成绩是70分以上（包括70分）的学生中选一人，求选到第一名学生的概率（第一名学生只一人）.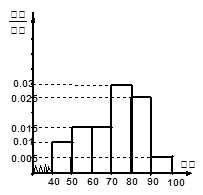

科目数学题型解答题难度中等

知识点：误差估计

设直线 $l_{1} : y = k_{1} x + 1, l_{2} : y = k_{2} x - 1$ ,其中实数 $k_{1}, k_{2}$ 满足 $k_{1} k_{2} + 2 = 0$ ,
（I）证明 $l_{1}$ 与 $l_{2}$ 相交；
（II）证明 $l_{1}$ 与 $l_{2}$ 的交点在椭圆 $2 x^{2} + y^{2} = 1$ 上.

在 $△$ $A B C$ 中， $a$ = $\sqrt{3}$ ， $b =$ $\sqrt{2}$ ， $1 + 2 \cos (B + C) = 0$ ，求:

（1）角A的大小；

（2）边 $B C$ 上的高．

设函数 $f (x)$ 定义在 $(0, + \infty)$ 上， $f (1) = 0$ ，导函数 $f ` (x) = \frac{1}{x}$ , $g (x) = f (x) + f ` (x)$ .

（Ⅰ）求 $g (x)$ 的单调区间和最小值；

（Ⅱ）讨论 $g (x)$ 与 $g (\frac{1}{x})$ 的大小关系；

（Ⅲ）是否存在 $x_{0} > 0$ ，使得 $|g (x) - g (x_{0})| < \frac{1}{x}$ 对任意 $x > 0$ 成立？若存在，求出 $x_{0}$ 的取值范围；若不存在请说明理由。

如图，A地到火车站共有两条路径 $L_{1}$ 和 $L_{2}$ ，据统计，通过两条路径所用的时间互不影响，所用时间落在各时间段内的频率如下表：

时间（分钟）	$10 ~ 20$	$20 ~ 30$	$30 ~ 40$	$40 ~ 50$	$50 ~ 60$
$L_{1}$ 的频率	0.1	0.2	0.3	0.2	0.2
$L_{2}$ 的频率	0	0.1	0.4	0.4	0.1

现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站。
（Ⅰ）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（Ⅱ）用 $X$ 表示甲、乙两人中在允许的时间内能赶到火车站的人数，针对（Ⅰ）的选择方案，求 $X$ 的分布列和数学期望。

如图，从点 $P_{1} (0, 0)$ 作 $x$ 轴的垂线交曲线 $y = e^{x}$ 于点 $Q_{1} (0, 1)$ ，曲线在 $Q_{1}$ 点处的切线与 $x$ 轴交于点 $P_{2}$ ，再从 $P_{2}$ 作 $x$ 轴的垂线交曲线于点 $Q_{2}$ ，依次重复上述过程得到一系列点： $P_{1} ， Q_{1} ； P_{2} ， Q_{2} ； \dots ； P_{n} ， Q_{n}$ ,记 $P_{k}$ 点的坐标为 $(x_{k}, 0)$ $(k = 1, 2, \dots, n ）$ .

（Ⅰ）试求 $x_{k}$ 与 $x_{k - 1}$ 的关系（ $2 \leq k \leq n$ ）
（Ⅱ）求 $|P_{1} Q_{1}| + |P_{2} Q_{2}| + |P_{3} Q_{3}| + . . . + |P_{n} Q_{n}|$

试卷网试题网古诗词网作文网范文网