如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .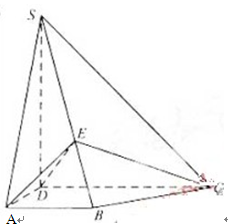
已知曲线
,直线
(t为参数)
(1)写出曲线
的参数方程,直线
的普通方程;
(2)过曲线 上任意一点 作与 夹角为30°的直线,交 于点A,求 的最大值与最小值.
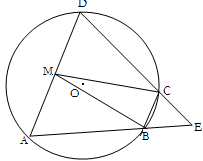
如图,四边形 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点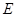 ,且
,且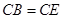 .
.
(I)证明: ;
;
(II)设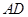 不是
不是 的直径,
的直径,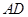 的中点为
的中点为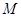 ,且
,且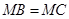 ,证明:
,证明: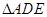 为等边三角形.
为等边三角形.
设函数
,曲线
处的切线斜率为0
求
;若存在
使得
,求
的取值范围。
已知点
,圆
:
,过点
的动直线
与圆
交于
两点,线段
的中点为
,
为坐标原点.
(1)求
的轨迹方程
(2)当
时,求
的方程及
的面积
如图,三棱柱
中,侧面
为菱形,
的中点为
,且
平面
.
(1)证明:
(2)若 , 求三棱柱 的高.