在数列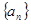 中,已知
中,已知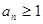 ,
,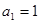 ,且
,且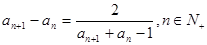 .
.
(1)记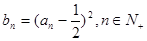 ,求证:数列
,求证:数列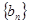 是等差数列;
是等差数列;
(2)求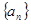 的通项公式;
的通项公式;
(3)对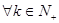 , 是否总
, 是否总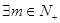 使得
使得 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知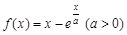 .
.
(Ⅰ)判断曲线 在
在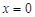 的切线能否与曲线
的切线能否与曲线 相切?并说明理由;
相切?并说明理由;
(Ⅱ)若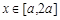 求
求 的最大值;
的最大值;
(Ⅲ)若 ,求证:
,求证: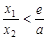 .
.
已知圆O: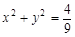 ,直线l:
,直线l: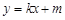 与椭圆C:
与椭圆C: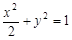 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.
(Ⅰ)若直线l过椭圆C的左焦点,且与圆O交于A、B两点,且 ,求直线l的方程;
,求直线l的方程;
(Ⅱ)如图,若 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.
如图,在直角梯形ABCD中, ,
,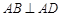 ,且
,且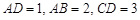 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面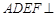 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.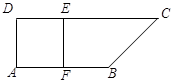
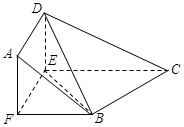
(Ⅰ)求证: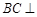 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求恰好第2次中奖的概率;
(Ⅱ)从中有放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
在 中,
中,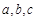 分别为内角
分别为内角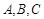 对边,且
对边,且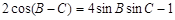 .
.
(Ⅰ)求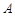 ;
;
(Ⅱ)若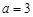 ,
,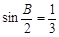 ,求
,求 的值.
的值.