如图,一次函数y=kx+b与反比例函数y=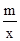 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
求一次函数与反比例函数的解析式;
根据所给条件,请直接写出不等式kx+b>
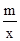 的解集
的解集过点B作BC⊥x轴,垂足为C,求S△ABC
先化简,再求值: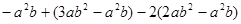 ,其中
,其中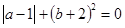 .
.
解方程(每题6分,共12分)
(1) 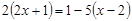 (2)
(2) 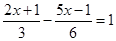
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组 的解,点C是直线
的解,点C是直线 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
如图,在梯形ABCD中,AB∥CD,∠BCD=90°, BD平分∠ABC
求证:(1) DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
(3) 在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求 的值.
的值.
甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每付定价20元,乒乓球每盒定价5元。现两家商店搞促销活动。甲店:每买一付球拍赠一盒乒乓球;乙店:按定价的9折优惠。某班级需购球拍4付,乒乓球若干盒(不少于4盒)。
(1)设购买乒乓球盒数为x(盒),在甲店购买的付款数为y甲(元),在乙店购买的付款数为y乙(元),分别写出在两家商店购买的付款数与乒乓球盒数x之间的函数关系式。
(2)就乒乓球盒数讨论去哪家商店买合算?